Sistem persamaan linear adalah persamaan-persamaan linear yang dikorelasikan untuk membentuk suatu sistem. Sistem persamaannya bisa terdiri dari satu variabel, dua variabel atau lebih. Dalam bahasan ini, kita hanya membahas sistem persamaan linear dengan dua dan tiga variabel.
Sistem Persamaan Linear Dua Variabel (SPLDV)
Sistem persamaan linear dua variabel adalah sistem persamaan linear yang terdiri dari dua persamaan dimana masing-masing persamaan memiliki dua variabel. Contoh SPLDV dengan variabel  dan
dan 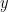 :
:
dimana  , dan
, dan  adalah bilangan-bilangan real.
adalah bilangan-bilangan real.
Penyelesaian SPLDV
Penyelesaian SP:DV bertujuan untuk menentukan nilai yang memenuhi kedua persamaan yang ada pada SPLDV. Penyelesaian SPLDV terdapat beberapa cara, yaitu:
Metode grafik
Pada metode grafik ini, langkah-langkah yang dilakukan pertama adalah menentukan grafik garis dari masing-masing persamaan kemudian menentukan titik potong dari kedua garis. Titik potong dari kedua garis tersebut adalah penyelesaian dari SPLDV.
Contoh Soal:
Tentukah penyelesaian dari SPLDV berikut:
Tentukah penyelesaian dari SPLDV berikut:
Jawab:
Langkah pertama tentukan garis dari masing-masing persamaan.
Langkah pertama tentukan garis dari masing-masing persamaan.

Setelah diperoleh grafik dari kedua persamaan, sekarang menentukan titik potong dari kedua garis dan menentukan koordinat dari titik potong tesebut.

Dari grafik sistem persamaan linear diatas diperoleh titik potong dengan koordinat  , sehingga penyelesaian dari SPLDV adalah
, sehingga penyelesaian dari SPLDV adalah 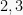 .
.
Untuk membuktikan penyelesaian dari SPLDV, penyelesaian tersebut kita subtitusikan ke persamaan dengan  dan
dan 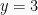 .
.
Pada metode grafik ini, terdapat beberapa jenis himpunan penyelesaian berdasarkan grafik persamaan, yaitu:
- Jika kedua garis berpotongan, maka perpotonga kedua garis adalah penyelesaian dari SPLDV dan memiliki satu penyelesaian.
- Jika kedua garis sejajar, maka SPLDV tidak memiliki penyelesaian
- Jika kedua garis saling berhimpit, maka SPLDV memiliki tak berhingga himpunan penyelesaian.
Metode eliminasi
Pada metode eliminasi ini, menentukan penyelesaian dari variabel  dengan cara mengeliminasi variabel
dengan cara mengeliminasi variabel 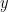 , dan untuk menentukan penyelesaian variabel
, dan untuk menentukan penyelesaian variabel 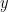 dengan cara mengeliminasi variabel
dengan cara mengeliminasi variabel  .
.
Contoh Soal:
Tentukah penyelesaian dari sistem persamaan linear dua variabel berikut:
Tentukah penyelesaian dari sistem persamaan linear dua variabel berikut:
Jawab:
Pertama menentukan penyelesaian dari variabel .
.
Pertama menentukan penyelesaian dari variabel
Mengeliminasi variabel 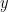 dapat dilakukan dengan mengurangi persamaan I dengan persamaan II.
dapat dilakukan dengan mengurangi persamaan I dengan persamaan II.
Diperoleh persamaan akhir 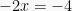 , bagi kedua ruas dengan -2, diperoleh penyelesaian
, bagi kedua ruas dengan -2, diperoleh penyelesaian  .
.
Kedua menentukan penyelesaian dari variabel 
Mengeliminasi variabel  dapat dilakukan dengan menjumlahkan persamaan I dengan persamaan II.
dapat dilakukan dengan menjumlahkan persamaan I dengan persamaan II.
Diperoleh persamaan akhir  , bagi kedua ruas dengan 2, diperoleh penyelesaian
, bagi kedua ruas dengan 2, diperoleh penyelesaian 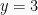
Sehingga himpunan penyelesaian dari SPLDV tersebut adalah  .
.
Metode substitusi
Pada metode substitusi, langkah pertama yang dilakukan adalah mengubah salah satu persamaan menjadi persamaan fungsi, yaitu  sebagai fungsi dari
sebagai fungsi dari 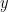 atau
atau 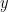 sebagai fungsi dari
sebagai fungsi dari  . Kemudian subtitusikan
. Kemudian subtitusikan  atau
atau 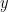 pada persamaan yang lain.
pada persamaan yang lain.
Contoh Soal:
Tentukah penyelesaian dari SPLDV berikut:
Tentukah penyelesaian dari SPLDV berikut:
Jawab:
Ubah persamaan (I) menjadi bentuk fungsi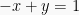 dengan memindahkan variabel
dengan memindahkan variabel  ke ruas kanan menjadi
ke ruas kanan menjadi  .
.
Ubah persamaan (I) menjadi bentuk fungsi
Kemudian persamaan fungsi 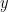 disubtitusikan pada persamaan (II), menjadi
disubtitusikan pada persamaan (II), menjadi  . Diperoleh persamaan
. Diperoleh persamaan  dan kurangi masing-masing ruas dengan 1, menjadi
dan kurangi masing-masing ruas dengan 1, menjadi 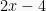 . Kemudian bagi kedua ruas dengan 2 menjadi
. Kemudian bagi kedua ruas dengan 2 menjadi  . Hasil variabel
. Hasil variabel  disubtitusikan pada salah satu persamaan awal, misal pada persamaan (I), menjadi
disubtitusikan pada salah satu persamaan awal, misal pada persamaan (I), menjadi 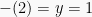 , jadi
, jadi 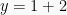 atau
atau 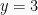 .
.
Sehingga himpunan penyelesaian sistem persamaan linear dua variabel nya adalah  .
.
Metode eliminasi-subtitusi
Metode ini adalah gabungan dari metode eliminasi dan subtitusi. Pertama eliminasi salah satu variabel, kemudian penyelesaian dari variabel yang diperoleh disubtitusikan pada salah satu persamaan.
Coba kerjakan soal di atas dengan menggunakan metode eliminasi-substitusi.
Sistem Persamaan Linear Tiga Variabel (SPLTV)
Sistem persamaan linear tiga variabel adalah sistem persamaan yang terdiri dari tiga persamaan dimana masing-masing persamaan memiliki tiga variabel. Contoh SPLTV dengan variabel 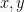 dan
dan  :
:
dimana 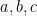 dan
dan 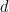 adalah bilangan-bilangan real.
adalah bilangan-bilangan real.
Pada SPLTV terdapat 2 cara penyelesaian, yaitu:
- Metode Subtitusi
Langkah yang dilakukan pada metode ini yaitu:
- Ubah salah satu persamaan yang ada pada sistem dan nyatakan
sebagai fungsi dari
dan
, atau
sebagai fungsi dari
dan
, atau
sebagai fungsi dari
dan
..
- Subtitusikan fungsi
atau
atau
dari langkah pertama pada dua persamaan yang lain, sehingga diperoleh SPLDV.
- Selesaikan SPLDV yang diperoleh dengan metode yang dibahas pada penyelesaian SPLDV di atas.
Contoh Soal:
Tentukan penyelesaian dari sistem persamaan linear tiga variabel berikut:
Tentukan penyelesaian dari sistem persamaan linear tiga variabel berikut:
Jawab:
Langkah pertama, nyatakan persamaan (I) menjadi fungsi dari  , yaitu:
, yaitu: 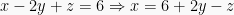 . Kemudian subtitusikan pada persamaan (II) dan (III), menjadi
. Kemudian subtitusikan pada persamaan (II) dan (III), menjadi
Persamaan (II): 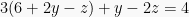
Selesaikan, didapat: 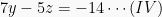
Persamaan (III): 
Selesaikan, didapat: 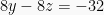 atau
atau  .
.
Persamaan (IV) dan (V) membentuk SPLDV
Dari persamaan (V),  , kemudian disubtitusikan pada persamaan (IV), menjadi:
, kemudian disubtitusikan pada persamaan (IV), menjadi:
Kemudian subtitusikan 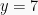 pada persamaan
pada persamaan  diperoleh
diperoleh atau
atau 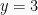 .
.
Subtitusikan 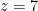 dan
dan  pada persamaan
pada persamaan  , menjadi
, menjadi 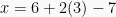 , diperoleh
, diperoleh 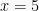 .
.
Sehingga himpunan penyelesaian adalah 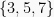
- Metode Eliminasi
Langkah penyelesaian pada metode eliminasi yaitu:
- Eliminasi salah satu variabel sehingga diperoleh SPLDV
- Selesaikan SPLDV yang diperoleh dengan langkah seperti pada penyelesaian SPLDV yang telah dibahas
- Subtitusikan variabel yang telah diperoleh pada persamaan yang ada.










![CONTOH SOAL SEJARAH WAJIB (Soal 2) [SEMESTER 2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgIiBdcn7U-yAVYHwp1iZQ_hhc9FwHvZ4HGKGseQolUc_XUq82nE4zHOKlwxU-9uJOiXZ1B8Ch9h5gPVkf6YGW2FoeCM6kBJ3XRFsyRf3Y4_VNnDkA2SCYCzD0-dmcNcPHJQcRF16RVpXvG/s72-c/post-sejarah.jpg)

![AKTIVITAS RITMIK [BAGIAN 2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjsY1k03vL3qqgUbNmPH2VTTSkT9PMcO2hoGljw-dYqYNPIhrn1jEn8o3NcBITit_lJITBhc7khUe2erCRHTR1oGTy6Yl1UrCi4yIUjU2cRUCO_pCb2Tsn3aiyO9r6rpHRqyZkqr6sJe21s/s72-c/senam-irama.jpg)


Tidak ada komentar:
Posting Komentar